Μαθηματικές-καλλιτεχνικές δημιουργίες

Πλησιάζοντας τα Χριστούγεννα και αφού είχαμε ολοκληρώσει την παράδοση του μαθήματος της τετραγωνικής ρίζας και του πυθαγορείου θεωρήματος, αποφασίσαμε με τους μαθητές της Β΄ Γυμνασίου να αφιερώσουμε τις τελευταίες διδακτικές ώρες του μαθήματος για το 2019, στη ζωγραφική! Με τη σπείρα των αρρήτων μάθαμε πως τους άρρητους αριθμούς δεν μπορούμε να τους υπολογίσουμε ακριβώς αλλά μπορούμε να τους σχεδιάσουμε! Με το δέντρο του Πυθαγόρα μάθαμε πώς μπορούμε να δώσουμε μορφή σε μία άπειρη διαδικασία!

 Τα έργα του Β1

 Τα έργα του Β2

Τα έργα του Β3

…και λίγες πληροφορίες..

Η Σπείρα των Αρρήτων

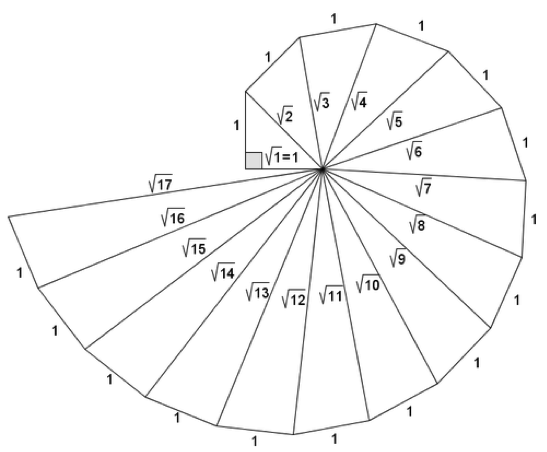
Στον περίφημο διάλογο του Πλάτωνα Θεαίτητος,ο Πλατών εξηγεί πως ο δάσκαλος των μαθηματικών του,ο Θεόδωρος ο Κυρηναίος απέδειξε την ιδιότητα του αρρήτου το 425 π.Χ. Με την βοήθεια του πυθαγορείου θεωρήματος ο Θεόδωρος κατασκεύασε την περίφημη σπείρα του. Μια σπείρα πού αποτελείται από  συνεχόμενα ορθογώνια τρίγωνα με υποτείνουσες τετραγωνικές ρίζες διαδοχικούς φυσικούς. Η κατασκευή ξεκίνα με ένα  ισοσκελές ορθογώνιο τρίγωνο με ίσες πλευρές μήκους 1 και υποτείνουσα  την τετραγωνική ρίζα του 2,κατόπιν δημιούργησε ένα νέο ορθογώνιο τρίγωνο με κάθετη πλευρά την υποτείνουσα του πρώτου και δεύτερη κάθετη πλευρά μήκους 1, η υποτείνουσα στο νέο ορθογώνιο ισούται με τετραγωνική  ρίζα του 3, η διαδικασία συνεχίζεται  ομοίως. Δείτε το σχήμα που προκύπτει :

Το Δένδρο του Πυθαγόρα

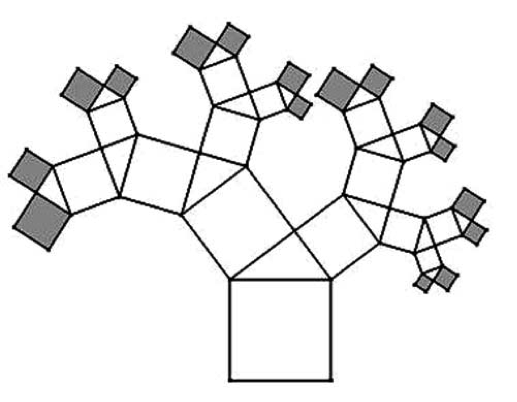
 Είναι ένα σπάνιο φυτό που φυτρώνει στο Ευκλείδειο επίπεδο.                                            

Ο κορμός του είναι ένα τετράγωνο, του οποίου η επάνω πλευρά είναι η υποτείνουσα ενός ορθογωνίου τριγώνου και στις κάθετες πλευρές αυτού του τριγώνου μεγαλώνουν τα κλαδιά, που είναι τετράγωνα τα οποία αντιστοιχούν σε αυτές.               

Κάθε ένα από τα δύο τετράγωνα με τη σειρά του αναπτύσσεται όπως ένα νέο δένδρο στο οποίο αναπτύσσεται ένα άλλο όμοια με την παραπάνω περιγραφή. Η διαδικασία αυτή είναι προφανές ότι μπορεί να συνεχιστεί άπειρες φορές...